Truncated 24-cell honeycomb

Truncated 24-cell honeycomb
(No image)
Type Uniform honeycomb
Schläfli symbol t0,1{3,4,3,3}
t0,1,2{3,3,4,3}
t1,2,3{4,3,3,4}
t1,2,3{4,3,31,1}
o{31,1,1,1}
Coxeter-Dynkin diagrams




4-face type tesseract
truncated 24-cell
Cell type cube
truncated octahedron
Face type Square
Triangle
Vertex figure
Regular tetrahedral pyramid
Coxeter groups 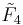{\tilde{F}}_4, [3,4,3,3]
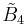{\tilde{B}}_4, [4,3,31,1]
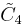{\tilde{C}}_4, [4,3,3,4]
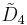{\tilde{D}}_4, [31,1,1,1]
Properties Vertex transitive

In four-dimensional Euclidean geometry, the truncated 24-cell honeycomb is a uniform space-filling honeycomb. It can be seen as a truncation of the regular 24-cell honeycomb, containing tesseract and truncated 24-cell cells.

It has a uniform alternation, called the snub 24-cell honeycomb. It is a true snub from the D4 construction. This truncated 24-cell is an omnitruncation, o{31,1,1,1}, and its snub is represented as s{31,1,1,1}.

Contents

Alternate names

Symmetry constructions

There are five different symmetry constructions of this tessellation. Each symmetry can be represented by different arrangements of colored truncated 24-cell facets. In all cases, four truncated 24-cells, and one tesseract meet at each vertex, but the vertex figures have different symmetry generators.

Coxeter group Full
symmetry
group		 Coxeter-Dynkin diagram Facets Vertex figure
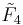{\tilde{F}}_4 = [3,4,3,3] [3,4,3,3] 4:
1:
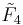{\tilde{F}}_4 = [3,3,4,3] [3,3,4,3] 3:
1:
1:
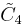{\tilde{C}}_4 = [4,3,3,4] [[4,3,3,4]] 2,2:
1:
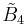{\tilde{B}}_4 = [31,1,3,4] <[31,1,3,4]> = [4,3,3,4] 1,1:
2:
1:
{\tilde{D}}_4 = [31,1,1,1] [3,3[31,1,1,1]] = [3,3,4,3] 1,1,1,1:

1:

See also

References